Since numerical computations based on the equations in section 2.3 are at an atomic level, they are historically limited to simple cases containing not too many degrees of freedom (Aharoni, 2000, p173). For larger problems other techniques must be used.
Brown (1963) suggested a theory which is referred to as
micromagnetic theory. Instead of considering individual
magnetic moments, a continuous magnetisation function
![]() is
used to approximate the atomic interaction described above. The
magnetisation represents the locally averaged density of magnetic
moments:
is
used to approximate the atomic interaction described above. The
magnetisation represents the locally averaged density of magnetic
moments:
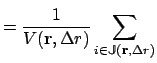 |
(2.16) |
where
![]() is a sphere of radius
is a sphere of radius ![]() placed at
placed at
![]() and
and
![]() is the set of indices:
is the set of indices:
| (2.17) |
for magnetic moments
![]()
![]() that are located inside the
volume
that are located inside the
volume
![]() .
.
This averaging can be performed over the scale of the exchange length (see equation 2.40) and will always contain many magnetic moments.
![]() is assumed to be a continuous and
differentiable function which allows the expression of the
interactions described above using differential operators. The
resulting equations can be solved analytically (if possible) or
numerically.
is assumed to be a continuous and
differentiable function which allows the expression of the
interactions described above using differential operators. The
resulting equations can be solved analytically (if possible) or
numerically.