Critical F: The value of the F-statistic at the threshold probability α of mistakenly rejecting a true null hypothesis (the critical Type-I error).
The F-statistic is the test statistic used in ANOVA and GLM, named in honour of R. A. Fisher, who first described the distribution and developed the method of analysis of variance in the 1920s. The continuous F distribution for a given set of test and error degrees of freedom is used to determine the probability of obtaining at least as large a value of the observed F-ratio of explained to unexplained variation, given a true null hypothesis. The associated P-value reports the significance of the test effect on the response in terms of the probability of mistakenly rejecting a true null hypothesis, which is deemed acceptably small if P < α, where α often takes a value of 0.05.
The P-value is the area under the F distribution to the right of the corresponding F value:

where p and q are the model test and error degrees of freedom respectively, and the
beta function ![]() If the integral limit FQ
exceeds the critical F-value F[α], then P
< α. Figure 1 shows two examples of the position
of the critical F-value along its F distribution. The distribution has a
strong positive skew for small test degrees of freedom, showing in Fig. 1(a).
If the integral limit FQ
exceeds the critical F-value F[α], then P
< α. Figure 1 shows two examples of the position
of the critical F-value along its F distribution. The distribution has a
strong positive skew for small test degrees of freedom, showing in Fig. 1(a).
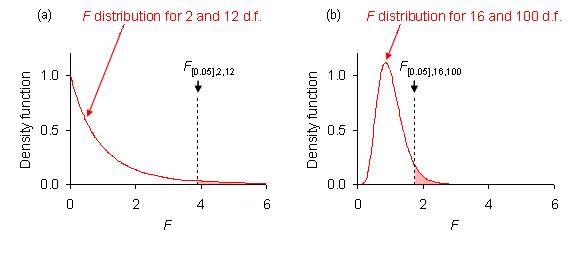
Fig. 1. In the absence of a treatment effect, the observed F = TMS/EMS follows the F distribution, here showing with α = 0.05 given by the red-shaded area under its right-hand tail above F[α]. (a) F[0.05],2,12 = 3.89; (b) F[0.05],16,100 = 1.75.
The program Ftable.exe provides critical values of the F distribution for a chosen α, and also the Type-I error probability associated with an observed value of F, given test and error degrees of freedom. For example, it will show critial F[0.05],2,12 = 3.89; and at an observed F2,12 = 3.98, P = 0.047.
Doncaster, C. P. & Davey, A. J. H. (2007) Analysis of Variance and Covariance: How to Choose and Construct Models for the Life Sciences. Cambridge: Cambridge University Press.
http://www.southampton.ac.uk/~cpd/anovas/datasets/